
>Dialog mit der Natur<
Zum 80. Geburtstag von Ilya Prigogine

Ilya Prigogine wurde am 25.Januar 1917 in Moskau geboren. Seine Familie siedelte 1921 nach Belgien über. 1941 wurde er in Chemie promoviert an der Freien Universität Brüssel, der er neben zahlreichen anderen Verpflichtungen -v.a. in Austin/Texas - bis heute als Lehrer und Forscher verbunden blieb. Für seinen Nachweis, daß einfache anorganische Moleküle sich spontan selbstorganisieren können zu einem höheren Komplexitätsgrad erhielt er 1977 den Nobelpreis für Chemie. Er ist sicherlich einer der großen Gelehrten unserer Zeit, nicht zuletzt auch wegen der enzyklopädischen Breite seines Wissens. Ein Hauptanliegen des folgenden Beitrages ist es, mögliche Ansatzpunkte dafür aufzuzeigen, wie Prigogines Ergebnisse und Überlegungen für unsere eigenen Diskussionen, sei es für das Mensch-Natur-Verhältnis, sei es für die Sozialismusfrage überhaupt fruchtbar gemacht werden könnte. Schön wärīs, damit auch andere zur weiteren Rezeption angeregt zu haben.
I.
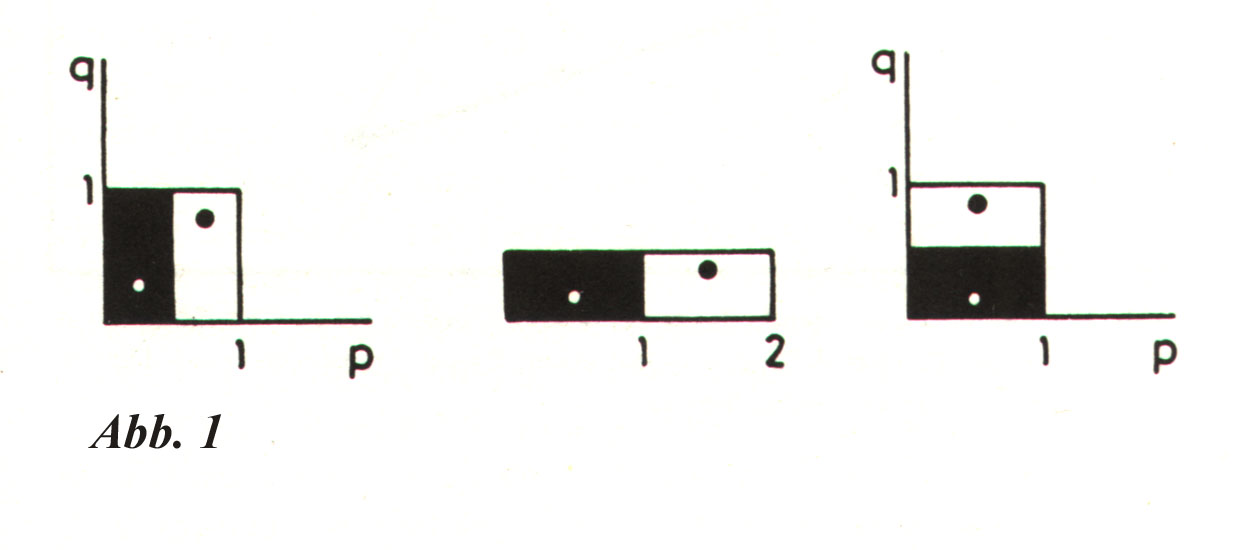
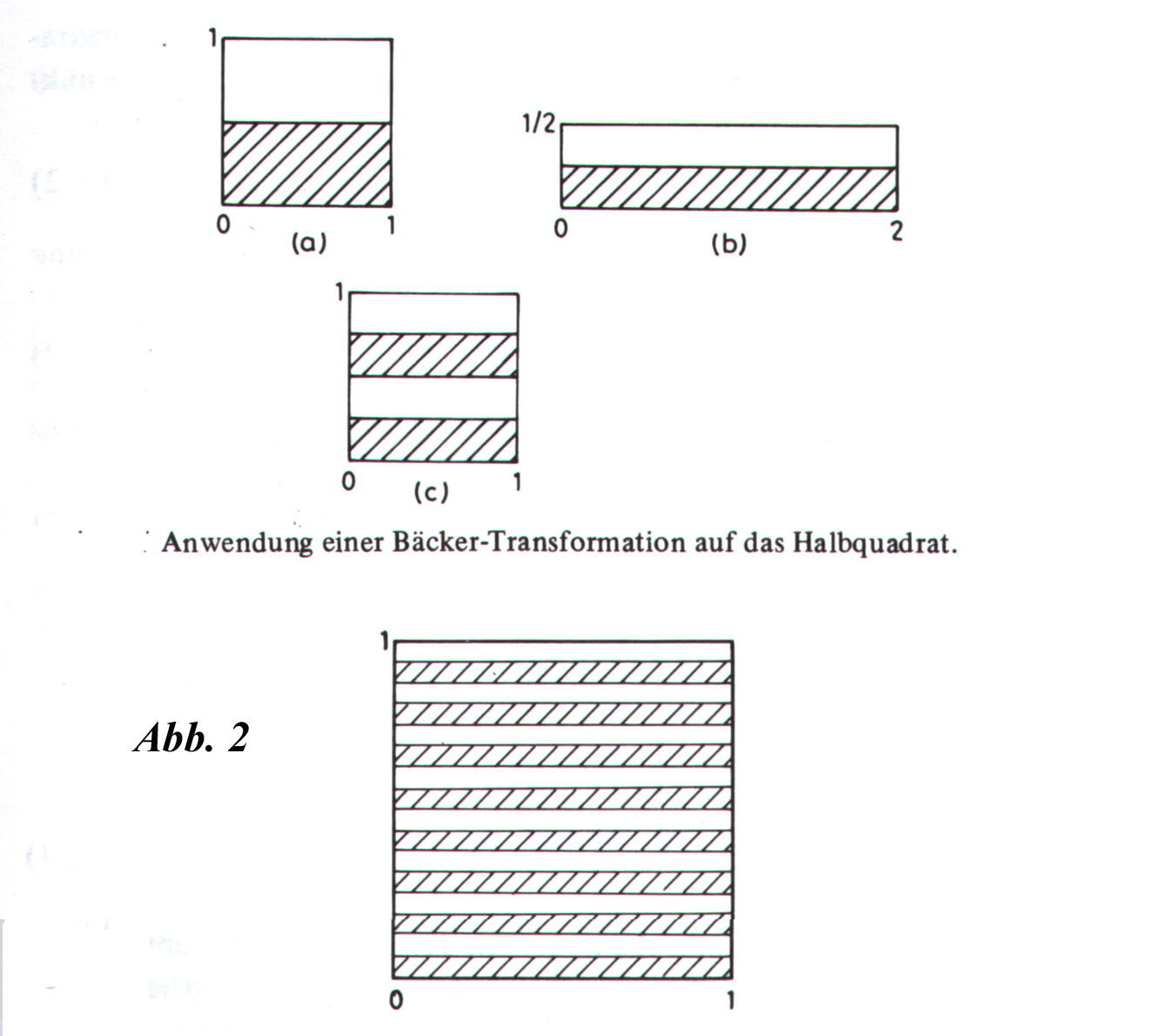
Man nehme eine quadratische Scheibe eines Rosinenbrotes, knautsche sie so zu einem Rechteck, daß ihre Höhe halbiert, dafür ihre Breite verdoppelt wird. Anschließend halbiert man das Rechteck durch einen vertikalen Schnitt und setzt die beiden Hälften übereinander, so daß wieder ein Quadrat ursprünglicher Größe vorhanden ist (vgl. Abb.1). Versehen mit entsprechendem mathematischem Brimborium haben wir soeben eine sog. Bäcker-Transformation ausgeführt. Verfolgt man bei der Hintereinanderausführung dieser Transformation den Weg (Trajektorie) einer einzelnen Rosine, stellen wir (determiniertes) Chaos fest: Wir finden sie mal hier mal dort, ohne jede Regelmäßigkeit, und zwei noch so dicht nebeneinanderliegende Rosinen landen an ganz unterschiedlichen Orten. Wir haben es mit einem instabilen dynamischen System zu tun. Global betrachtet entwickelt sich eine streifenförmige Fragmentierung der Fläche (Abb.2), d.h. bei jeder Transformation wird eine schraffierte Fläche in zwei getrennte aufgeteilt, so daß mit wachsender Zeit die Unterscheidung zwischen schraffierten und nicht schraffierten Flächen praktisch schwindet.
Das Verhalten dieses Systems läßt sich durch die Beschreibung der einzelnen Trajektorien nicht in den Griff kriegen, vielmehr ist dafür ein stochastisches, d.h. auf Wahrscheinlichkeiten beruhendes Konzept angesagt. Dazu hat die Arbeitsgruppe um Prigogine einen Operator eingeführt, der Bezug nimmt auf die Fragmentierung der Quadratfläche und so etwas wie eine innere (im Unterschied zur äußeren kinematischen) Zeit, ein "Alter", gerichtete Zeit also, repräsentiert und die man phänomenologisch am Fragmentierungszustand der Streifen ablesen kann.
Die Bäcker-Transformation läßt sich insofern noch als klassisches dynamisches System auffassen, als sich die Zeit der Trajektorien der Rosinen mit positivem und negativen Vorzeichen versehen läßt (also nicht an einen Zeitpfeil gebunden ist); denn es existiert ein sog. inverser Operator: führt man von einem bestimmten Zustand die Transformation "rückwärts" aus, landet man wieder am Ausgangszustand, was anschaulich sofort einleuchtet. Bei einer (mathematisch) verwandten, noch einfacher anmutenden Transformation, der sog. Bernoulli-Verschiebung, die nicht auf einer Fläche, sondern auf dem Zahlenstrahl operiert, ist das nicht der Fall: Nehmen wir eine beliebige Zahl zwischen 0 und 1, multiplizieren wir sie mit 2; geht das Ergebnis über 1 hinaus, wird 1 abgezogen. (Bsp.: 0.13, 0.26, 0.52, 0.04, 0.08, ...). Die entstehende Folge ist chaotisch. Auch hier läßt sich wie bei der Bäcker-Transformation mit Hilfe einer stochastischen Verteilungsfunktion ein Entwicklungsoperator definieren, der aber kein Inverses besitzt. Auch dies leuchtet sofort ein: Versuchen wir in unserem Beispiel von 0.04 "rückwärts" zu gehen, d.h. durch 2 zu teilen, landen wir woanders und ziemlich schnell bei 0 (der Versuch, das Abziehen der 1 durch eine Addition der 1 auszugleichen, führt immer zu einem Ergebnis größer als 1). Es gibt kein Zurück. Der Vorgang ist irreversibel. Die Zeitsymmetrie der klassischen Dynamik ist gebrochen: Die negative Zeit führt zu einem Attraktor (s. Kasten), der 0 nämlich, die positive zur Gleichförmigkeit (hinsichtlich der Verteilung).
Was lehrt uns das? Das Problem, die Entwicklung eines dynamischen Systems zu beschreiben, ohne sich sich auf Trajektorien zu stützen, hat sich bereits in der Quantenmechanik gestellt. Auch daß Syteme chaotisch werden können, kennt man aus der Hydrodynamik (Turbulenzen), wo die Beschreibung des Systems durch einzelne Trajektorien an seiner Komplexität zu scheitern scheint. Aber - und dies ist das Neue - durch diese einfachen Modelle wird aufgedeckt, daß Chaos, Instabilität, Irreversibilität weder der Komplexität noch der mangelnden Kenntnisse über die Anfangsbedingungen geschuldet sondern fundamentale Erscheinungen sind. Vorstellungen, daß Irreversibilität eine Illusion sei (Einstein), etwas was subjektiv durch den Beobachter hineingetragen würde, sind widerlegt. Darüber hinausgehend stehen die Dinge heute eher so, daß Chaos, Instabilität, Irreversibilität gerade als das "Normale" angesehen werden müssen, stabile und reversible Systeme dagegen als Grenz/Ausnahmefälle. Wenn wir diesen Normalfall also nicht dem Komplexen in die Schuhe schieben können, erwächst dieses dadurch nicht zu einem Problem, dem wir nur noch in banaler Resignation ("Es wird ja alles immer unübersichtlicher") zu begegnen neigen, wo doch angemessene Konzepte, zumindest die Entwicklung eines angemessenen Problembewußtseins so dringend nötig sind? Bevor es darum geht, ist auf einen weiteren Strang der Prigogineschen Gedankenwelt einzugehen.
II.
Als Engels den mechanischen Materialismus für überholt erklärte, führte er als Argument für den neuen, dialektischen Materialismus drei damals neuere Bereiche der Naturwissenschaften an: den Energieerhaltungssatz, der die "Einheit aller Bewegung in der Natur" begründet, die Entdeckung der organischen Zelle, die "der Entstehung, dem Wachstum und der Struktur der Organismen ... das Geheimnis" abstreift und die Darwinsche Entwicklungstheorie der Arten (MEW 20, S.467f. u. S.316f.). Bemerkenswert ist, daß alle genannten Errungenschaften mit Irreversibilität zu tun haben.
Irreversibilität rückte mit der Thermodynamik (Wärmelehre) ins Blickfeld und fand seinen Niederschlag v. a. im sog. Entropiesatz. Der Begriff Entropie ist sinnvoll nur anwendbar auf Systeme mit großer Elementanzahl (Atome, Moleküle) und läßt sich anschaulich fassen als ein Maß für die Unordnung der Elemente. Der Entropiesatz besagt nun, daß die Entropie eines isolierten Systems ohne Energiezuführung nicht geringer werden kann. Gasmoleküle z.B., die anfänglich in einem bestimmten Bereich eines Behälters konzentriert sind, werden sich im Laufe der Zeit gleichmäßig im Raum verteilen; der umgekehrte Vorgang, daß sich die Moleküle spontan an irgendeinem Ort konzentrieren wurde nie beobachtet. Unter stochastischem Aspekt ist der Zustand der gleichmäßigen Verteilung der "wahrscheinlichste" von allen Zuständen. Ist das Gleichgewicht hergestellt, ist die Irreversibilität, somit die Brechung der Zeitsymmetrie aufgehoben.
Um den Entropiesatz, der auch so formuliert wird: "Ein Perpetuum mobile, d.h. eine Maschine, mit der sich in Wärme umgewandelte Energie vollständig in mechanische zurückverwandeln läßt, ist unmöglich", ranken sich eine Fülle von Überlegungen und Spekulationen. Eine der ersten war die Hypothese vom "Wärmetod des Universums". Es wurde aber auch versucht, seinen Gehalt für die Bearbeitung ökonomisch-ökologischer Grundfragen fruchtbar zu machen. Als Beispiel von marxistischer Seite sei Altvaters "Die Zukunft des Marktes" genannt. Es läßt sich vielleicht darüber streiten, wie weit es gelungen ist, über eine thermodynamische Rhetorik hinauszukommen; aber selbst einer rein metaphorischen Verwendung des Entropiesatzes käme das Verdienst zu, ein Problem in aller Schärfe zu stellen: jeder stoffliche Umsatz ist nicht oder nur unter Zuführung externer Energie reversibel; ein vollständiges Recycling unserer Ressourcen ist unmöglich.
Während sich die bisherige Darstellung auf Verhältnisse nahe dem Gleichgewicht bezog - und das ist ja auch der klassische Gegenstand des Entropiesatzes - sind in den letzten Jahrzehnten v. a. durch Prigogine und seine Gruppe Systeme weitab vom Gleichgewicht in den Mittelpunkt des Interesses gerückt. Die "Fluctuations" (meistens mit "Schwankungen" übersetzt), die in Gleichgewichtsnähe flüchtiger Natur sind und an der Entropiezunahme oder -konstanz nichts ändern, können in offenen Systemen fernab vom Gleichgewicht eine "konstruktive" Funktion haben: sie können zu anderer oder neuer Ordnung führen. Prigogine nennt unter solchen Bedingungen sich bildende Strukturen dissipativ (weil durch Dissipation, d.h. Zerstreuung von Energie Erniedrigung der Entropie erreicht werden kann).
Die Möglichkeit eines breiten Spektrums makroskopischer Verhaltensweisen konnte seine Gruppe konstruieren anhand eines theoretischen Modells, dem sog. Brüsselator (nach dem Ort ihres Arbeitsplatzes benannt), der einem bestimmten Schema chemischer Reaktionen entspricht. Je nach Verhalten charakteristischer Parameter nimmt das System einen stationären Zustand (eine zeitlich unveränderte Nichtgleichgewichtssituation) an, wird instabil und "verzweigt" bei einem kritischen Wert in einen anderen inhomogenen oder stationären Zustand. In der Nähe der Verzweigunspunkte (Bifurkationen) bestimmen die Fluctuations/Schwankungen, auf welchem Zweig das System sich weiterbewegt, während zwischen zwei Verzweigungspunkten die Gesetze der chemischen Kinetik ausschlaggebend sind, so daß jede Beschreibung eines Systems, das Verzweigungen enthält, einen stochastischen Anteil (für die Schwankungen) und einen deterministischen (für die Reaktionsgleichungen) enthält.
Die eigentliche Welt der Selbstorganisation in dem Sinne, daß durch Schwankungen neue Ordnungen entstehen, beginnt, wenn die Schwankungen in einem gewissen, hier nicht näher zu erläuternden Sinne nicht mehr "normal" verteilt sind. Die Abweichung von der normalen Verteilung hängt wesentlich von der Größenordnung der Schwankungen in Bezug auf die Größe des Systems ab, vergleichbar mit der Keimbildung eines Flüssigkeitstropfens in einem übersättigten Dampf, der unterhalb einer kritischen, "embryonalen" Größe instabil und oberhalb dieser Größe wächst und den Dampf in Flüssigkeit verwandelt.
Der Brüsselator blieb nicht nur reine Theorie. So können Eigenschaften dissipativer Strukturen nachgewiesen werden in realen chemischen Reaktionen, in der Biologie bei Zellvorgängen oder der Bildung von Termitenhügeln, aber auch bei sozialen Prozessen wie z.B. der Urbanisierung, wo die Stadt als dissipative Struktur gefaßt wird. Natur- und Gesellschaftswissenschaften rücken näher zusammen. Das oben beschriebene Wechselspiel zwischen kurzreichweitigen Wechselwirkungen mit globalen Verhältnissen läßt sich als Paraphrase des Marxschen Diktums lesen, daß die Menschen in unabhängig von ihrem Willen existierende Verhältnisse gestellt sind, in die sie verändernd eingreifen, wenn die Zeit reif ist; oder - präziser - es thematisiert folgende (von Prigogine selbst zitierte!) Fragestellung von Althusser/Balibar: "... mit Hilfe welchen Konzeptes läßt sich der neue Determinationstyp denken, der soeben als Determination von Phänomenen einer Region, die durch die Struktur dieser Region vorgegeben war, identifiziert wurde? Allgemeiner: mit Hilfe welchen Konzeptes oder Ensembles von Konzepten läßt sich die Determination von Elementen einer Struktur, lassen sich die strukturellen Beziehungen zwischen diesen Elementen und alle Auswirkungen dieser Beziehungen durch die Wirksamkeit dieser Struktur denken? Und, a fortiori, mit Hilfe welchen Konzeptes oder welchen Ensembles von Konzepten läßt sich die Determination einer untergeordneten Struktur durch die dominante denken? Anders gesagt: Wie ist das Konzept einer strukturellen Kausalität zu definieren?" Diese eingeforderte neue Kausalität erfaßt aufgrund ihres Einschlusses von Möglichkeitsfeldern an Bifurkationspunkten, der Gegenüberstellung irreversibler Phasen und Reversibilität in Gleichgewichtssituationen, von Bereichen, in denen ein Attraktor wirksam wird, einen solchen Beziehungsreichtum, daß sie dazu beitragen kann, auch unseren Diskurs auf der Höhe der Zeit zu führen.
Die Kategorie "strukturelle Kausalität" ist für Dialektiker keineswegs etwas grundsätzlich Neues oder gar Fremdes. Im Gegenteil: gerade ihr Beziehungsreichtum ist es ja, der es ermöglicht, dialektische Figuren wie Umschlag von Quantität in Qualität, Einheit von Identität und Nichtidentität schärfer zu fassen bzw. zu "rationalisieren" und einzubetten in die letztlich nicht in die Einzelwissenschaften aufzulösende "Wissenschaft des Gesamtzusammenhangs", als was wir die Dialektik seit Engels verstehen. Mit den dissipativen Strukturen wird eine Natur beschrieben, die sich entwickelt, etwas Neues hervorbringt, "historisch" ist. Prigogine/Stengers weisen selbst daraf hin, daß Marx und besonders Engels die Idee einer Geschichte der Natur als integrierenden Bestandteil ihres Materialismus vertreten haben. Es ist unter diesem Aspekt zu prüfen - und damit kommen kommen wir auf die Engelsschen Überlegungen vom Anfang dieses Kapitels zurück - inwieweit die Dialektik mit der Theorie irreversibler Prozesse (in denen Reversibilität als Sonderfall enthalten ist) zusammenfällt.
III.
Was uns auf den Nägeln brennt, ist die Notwendigkeit, Organisationsformen zu finden, die Schluß machen mit der Tendenz zur Zerstörung der sozialen und natürlichen Lebensgrundlagen. Es stellt sich dabei die Frage, inwieweit wir nicht auch im Bereich menschlicher Konstruktion Selbstorganisation an die Stelle von Organisation treten lassen können. Der bisherige Sozialismus hat die Rolle der Selbstorganisation sicherlich vernachlässigt. Der Kapitalismus war ihm hier, durch die Ausnutzung des Wertgesetzes, überlegen, allerdings durch einen Vorzug, der sehr begrenzter Natur ist und gerade durch diese Begrenztheit Quelle desaströser Verwerfungen war und ist. Kennzeichnend für ihn ist nämlich eine lokale Ordnung/Effektivität, die - in thermodynamischer Metaphorik gesprochen - ihre Entropie exportiert: Der einzelne Betrieb geht zwar äußerst sparsam/effektiv mit Arbeitszeit und Material um, entledigt sich jedoch des Problems der internen überflüssigen Arbeitszeit durch Freisetzung der Arbeitskräfte nach außen - mit all ihren sozialen Folgen - und hinterläßt eine weitgehend unkontrollierte Vernutzung natürlicher Ressourcen. Dies reproduziert sich auf der Ebene kapitalistische Zentren - Entwicklungsländer und findet seinen vielleicht sinnfälligsten Ausdruck im Giftmüllexport in die armen Länder.
Die Herstellung von Gebrauchswerten durch Arbeit und die damit einhergehende Naturveränderung ist unabdingbar für menschliches Leben. Ihre historisch begrenzte Form des (Tausch-)Werts stellt eine Schranke dar, die uns daran hindert, unsere natürlichen Lebensgrundlagen zu sichern. Wenn wir den Kapitalismus abgekürzt als Herrschaft der abstrakten Arbeit fassen (Das Kapital interessiert die lebendige Arbeit des Arbeiters nur insoweit, wie sie sich in abstrakte umwandeln und als Tauschwert realisieren läßt.) rückt folgender Aspekt des Mensch-Natur-Verhältnisses ins Schlaglicht: Eingedenk der - in dieser Allgemeinheit unter Marxisten wohl unbestrittenen - Voraussetzung, daß Rechtsnormen, politische Entscheidungen, usw. samt ihrer ideologischen Rechtfertigungen vom Kapital strukturell dominiert sind, hängt die Besiedelung einer Landschaft, die Entscheidung über die Vernutzung einer Naturressource letztlich und entscheidend von einer Regelgröße, dem Wert ab. Wert ist aber eine rein gesellschaftliche Kategorie; die Natur produziert keine Werte. Daraus folgt, daß das kapitalistische Gesellschaftssystem gegenüber seiner natürlichen Umwelt selbstreferentiell, d.h. auf sich selbst rückbezogen ist. (Kurzfassung: Kapital ist selbstverwertender Wert!) Es hört zwar täglich die ökologischen Kassandrarufe, es fehlt auch nicht einmal der Glaube daran, allein es ist unfähig darauf zu reagieren.
Erst die Befreiung der Gebrauchswerte von ihrer kapitalistischen Hülle, erst wenn also die Ergebnisse der Arbeit mit ihren Zwecken übereinstimmen, eröffnet sich die Möglichkeit, auch die mit ihr einhergehende unumgängliche Transformation von Stoffen und Energien in Raum und Zeit zum Gegenstand menschlicher Konstruktion zu machen. Dies nun mit dem Konzept einer zentralen Planung versuchen zu wollen würde anmuten wie der Versuch, einen komplexen thermodynamischen Vorgang miskroskopisch durch die Beschreibung einzelner Trajektorien in den Griff zu bekommen. (Wo sollte auch in einem eh nur global zu denkenden Kommunismus das Zentrum sein?) Davon ist Abschied zu nehmen zugunsten einer selbstorganisierenden Planwirtschaft: selbstorganisatorisch, weil komplexe Vorgänge dann nur von ganz allgemeinen Vorschriften und wenigen Parametern abhängen, über die nur planvolles Vorgehen entscheiden kann.
Dies scheint mir unabdingbar dafür zu sein, daß neue Wege im "Dialog mit der Natur", die Prigogine aufgezeigt hat und die er auf der Ebene des experimentellen Frage- und Antwortspiels mit der Natur versteht, in ein praktisch-materielles Mensch-Natur-Verhältnis einmünden.
Attraktor: Anziehungspunkt,der in einem bestimmten Bereich unwiderstehlich wirkt. Rollt z.B. eine Kugel das Parabeltal hinunter (a)), landet sie nach einigen Abweichungen nach links und rechts im Talpunkt. Liegen zwei Täler vor (b)), scheidet der Bergpunkt im Koordinatenursprung die Attraktorbereiche des linken und des rechten Talpunktes.
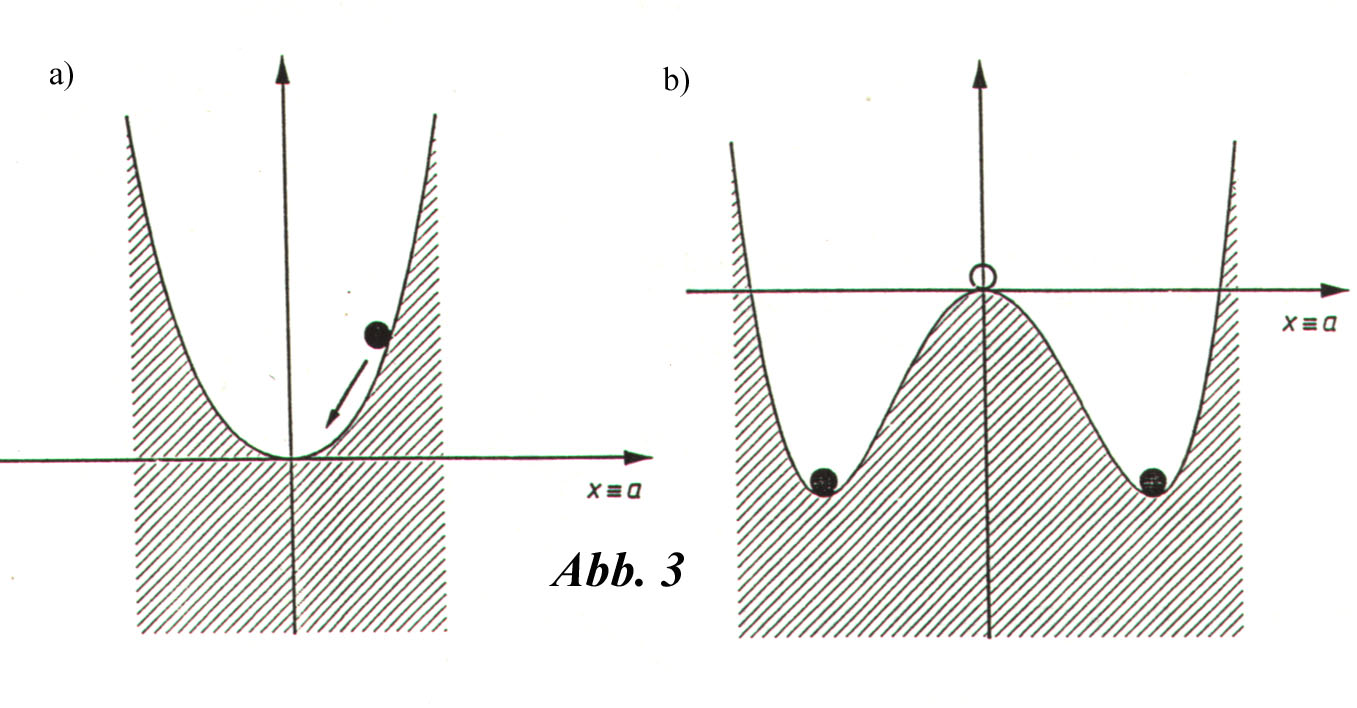
Ein einfaches Beispiel aus er Thermodynamik: Für isolierte Systeme ist das thermodynamische Gleichgewicht ein Attraktor für Nichtgleichgewichtszustände.
Literatur:
Ilya Prigogine/Isabelle Stengers, Dialog mit der Natur, Serie Piper, München 1993
Ilya Prigogine, Vom Sein zum Werden, Piper Münschen Zürich 1992
Ilya Prigogine, Die Gesetze des Chaos, Campus Verlag, Frankfurt(M)/New York 1995
Zur expliziten Bezugnahme auf soziale Systeme:
Ilya Prigogine, LīOrdre par Fluctuations et le Système Social, Rheinisch-Westfälische Akademie der Wissenschaften, Vorträge N 260
Abbildungen
Abb.1 aus: Dialog mit der Natur
Abb.2 aus: Vom Sein zum Werden
Abb. Zum Kasten "Attraktor" aus: Hermann Haken,Die Selbststrukturierung der Materie, Braunschweig 1991
Helmut Dunkhase, Berlin im Juli 1997