Liebe Leute vom Profilkurs Mathematik!

Das Merkwürdige am Fundamentalsatz der Algebra ist, dass er sich mit den Mitteln der Algebra allein gar nicht beweisen lässt. Ohne Stetigkeit läuft nichts. Die Beweise benutzen entweder Mittel der (komplexen) Funktionentheorie oder - wie hier - Argumente der Topologie (das ist der Zweig der Mathematik, der sich mit "stetigen" Verformungen beschäftigt). Schon hieraus ergibt sich, dass ein richtiger Beweis den Rahmen der Schulmathematik weit übersteigt. Es geht hier "nur" um Plausibilitätsbetrachtungen und danach - im Unterricht - um den Beweis von Teilaussagen.

Eine Quelle ist nachzutragen: Fig.3 ist aus Helmut Dittmann, Komplexe Zahlen, Bayerischer Schulbuchverlag 1981, S.97

Bei Problemen Mail an hDunkhase@t-online.de

Die folgende Site lässt sich als WORD-Datei downloaden

PK-MA Illustrationen zum Fundamentalsatz der Algebra

Zunächst Allgemeines über komplexe Funktionen.

Eine komplexe Funktion lässt sich auffassen als Abbildung einer Ebene auf eine andere Ebene. Wir bezeichnen die Urbildebene als z-Ebene und die Bildebene als w-Ebene. Komplexe Funktionen lassen sich als Ganzes nicht anschaulich darstellen wie die reellen, weil dazu vier Dimensionen bräuchte.

Eine gewisse Anschauung lässt sich dennoch gewinnen, wenn man die Bilder einzelner Linienstücke der z-Ebene studiert. Gut geeignet dafür sind Kreise, denn sie lassen sich einfach beschreiben und bei stetiger Vergrößerung des Radius wird die ganze Ebene überstrichen.

Wir betrachten nun einige Funktionen.

    2. Diese Funktionen ist nicht sonderlich interessant. Sie billdet jeden Punkt der z-Ebene auf den gleichen Punkt der w-Ebene ab.

Wir lassen auf der z-Ebene längs des Einheitskreises, beginnend bei , laufen und betrachten das Bild.

Wir erinnern daran, dass Multiplikation zweier komplexer Zahlen Multiplikation ihrer Beträge und Addition ihrer Argumente bedeutet. (Bei der Funktion verdoppeln sich also die Argumente.)

Der Anfangspunkt wird abgebildet auf , also auf sich selbst. Weiter finden wir:

(vgl. Fig.1)

 

Fig.1

 

 

Wenn die Hälfte des Kreises in der z-Ebene durchlaufen ist, ist in der w-Ebene schon der ganze Kreis durchlaufen. Weiter:

Also: Wird der Kreis in der z-Ebene einmal durchlaufen, so wird er in der w-Ebene zweimal durchlaufen.

Ist nun k ein Kreis mit einem beliebigen Radius r, so wird wegen der Radius des Bildkreises das Quadrat des Urbildradius. Für sieht das so aus:

 

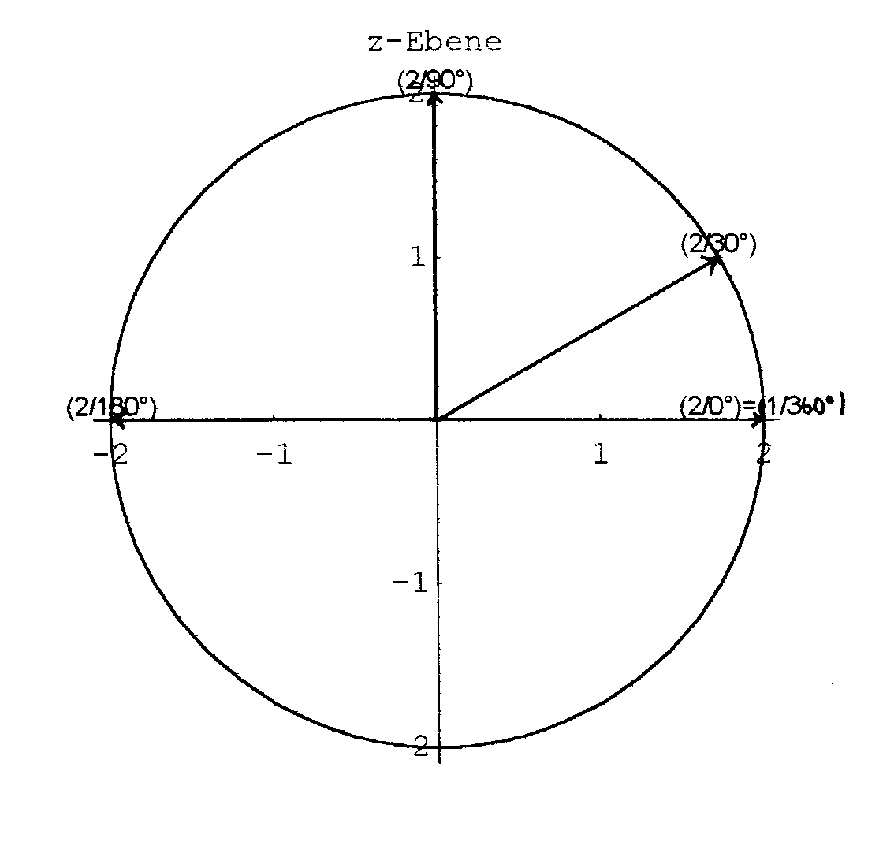
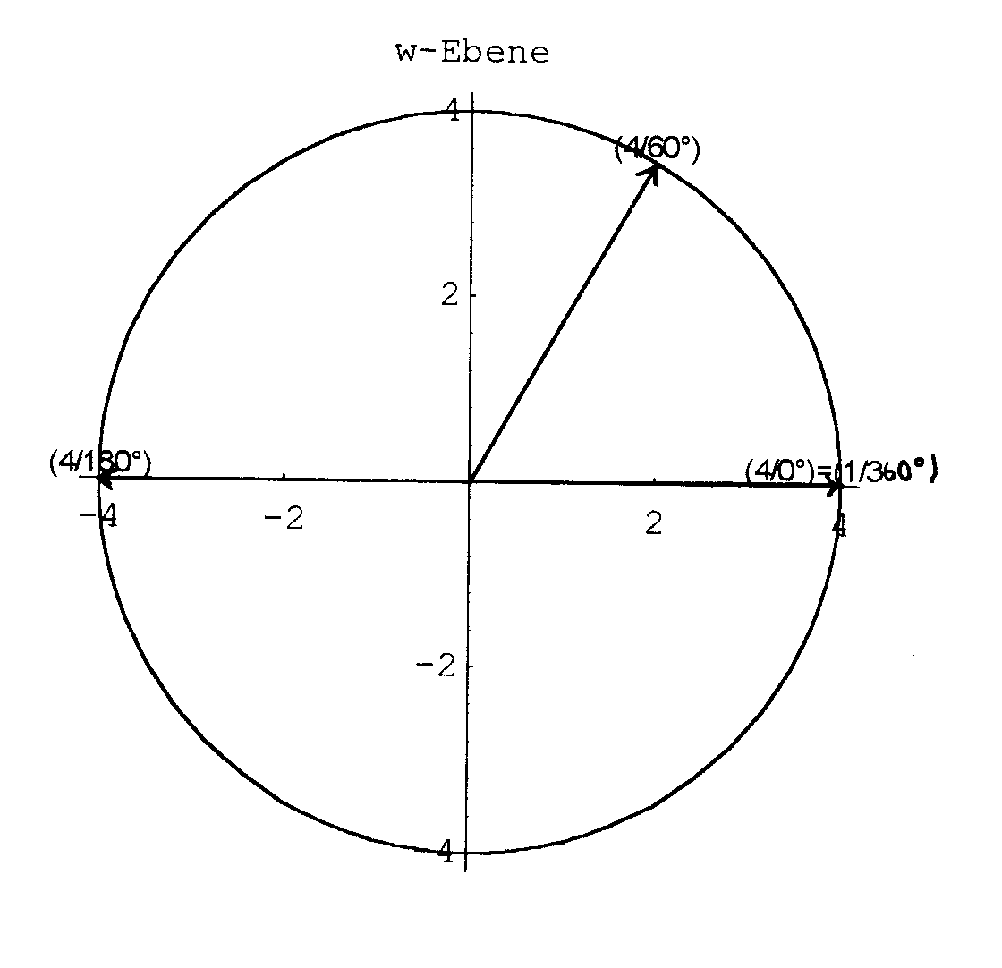
Fig.2

    2. Wegen ist das Bild der n-mal durchlaufende Kreis mit dem Radius .

Wir denken uns den Vektor am Ursprung der w-Ebene festgenagelt. An seine Spitze binden wir den Vektor z, so dass die Spitze des zusammengesetzten Vektors auf den Punkt w deutet.

Durchläuft nun z in der z-Ebene den Einheitskreis einmal, so rotiert auch unser "Vektormechanismus" in der w-Ebene. Während der Vektor aber zwei volle Umdrehungen ausführt, vollführt der an seine Spitze gebundene Vektor z nur eine. Das Ergebnis ist in Fig.3 dargestellt. Der gestrichelte Kreis ist das Bild des Einheitskreises unter der Funktion (zweimal durchlaufen). Die mit 0,1,2,...,16 bezeichneten Punkte geben die Orte von nach je Umdrehungen des Vektors z an. Es entsteht eine in sich geschlossene Kurve, die den Ursprung zweimal umschlingt.

Fig.3

5.

Wir erwarten eine Bildkurve, die sich irgendwie viermal um den Ursprung wickelt. Das Bild des Einheitskreises sieht aber so aus:

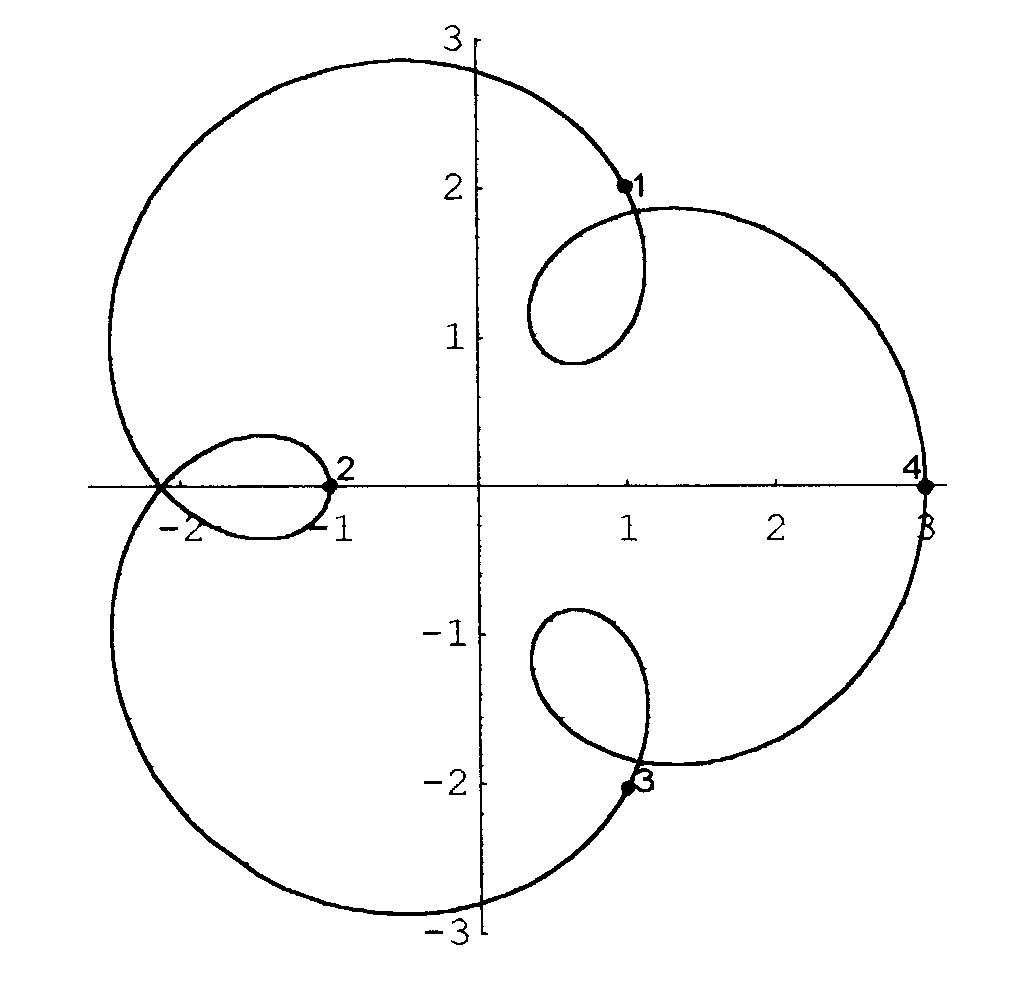
Fig.4

Die Zahlen geben die Umdrehungen der Bildkurve an.

Analysen wir das Ergebnis:

Das Bild des Ausgangspunktes ist , also . Nach der 2. Umdrehung der Bildkurve ist der Bildpunkt bei angekommen: Während schon 2 Umdrehungen hintersich hat, hat 2z erst eine halbe Umdrehung zurückgelegt. Nach einer halben Umdrehung steht der Zeiger von 2z aber auf . Der Bildpunkt ist also das Ergebnis von (in kartesischen Koordinaten:

). Der Term 2z stört also die Kreise des Terms für so sehr, dass der Ursprung nicht 4-mal, sondern nur einmal umschlungen wird.

Schon für sieht die Bildkurve ganz anders aus (Im Inneren sieht man noch einmal zum Vergleich das Bild des Einheitskreises):

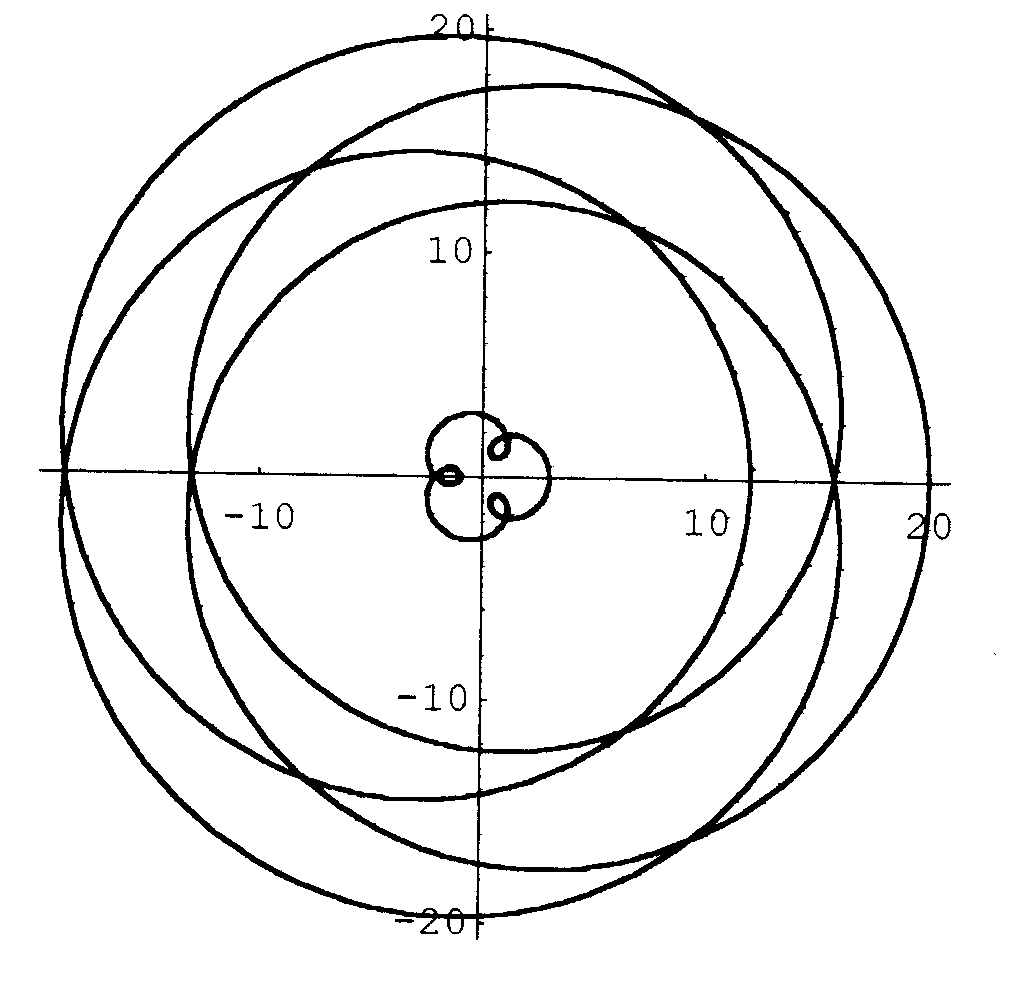
Fig.5

 

Aufgabe: Trage die Umdrehungszahlen ein.

Wenn wir bedenken, dass der Radius von gleich ist und der von 2z gleich 4, ist das Ergebnis plausibel.

Für große r setzt sich die höchste Potenz letztlich durch: Für betragsmäßig große z gleicht die Funktion immer mehr der Funktion .

 

 

***

 

 

 

 

Der Fundamentalsatz der Algebra besagt:

Jede Gleichung n-ten Grades

mit C hat wenigstens eine Lösung.

Wir machen uns die Beweisidee anhand der Funktion plausibel. (Eine Funktion mit wäre uninteressant, weil immer Lösung wäre.)

Wie das Bild für r=1 aussieht, zeigt Fig.6:

 

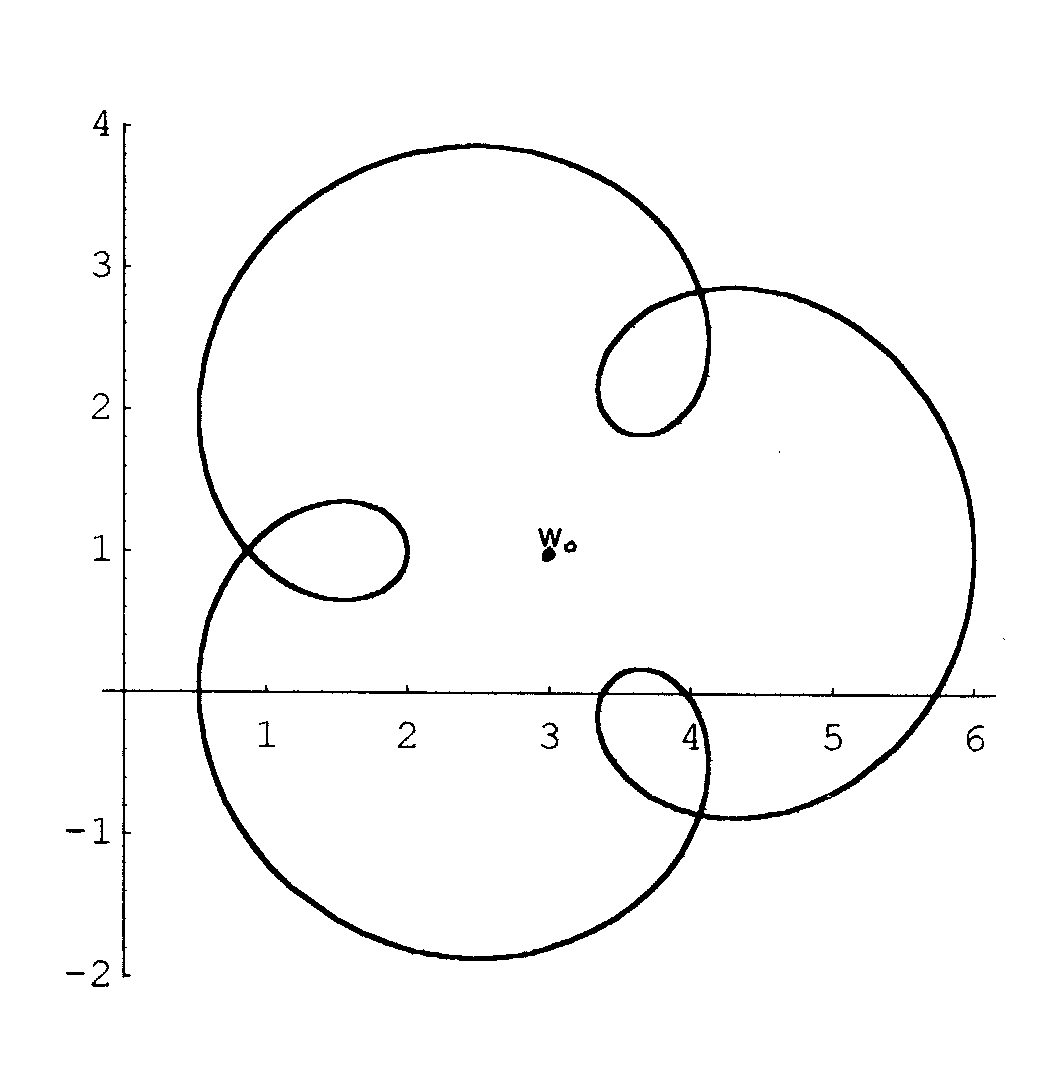
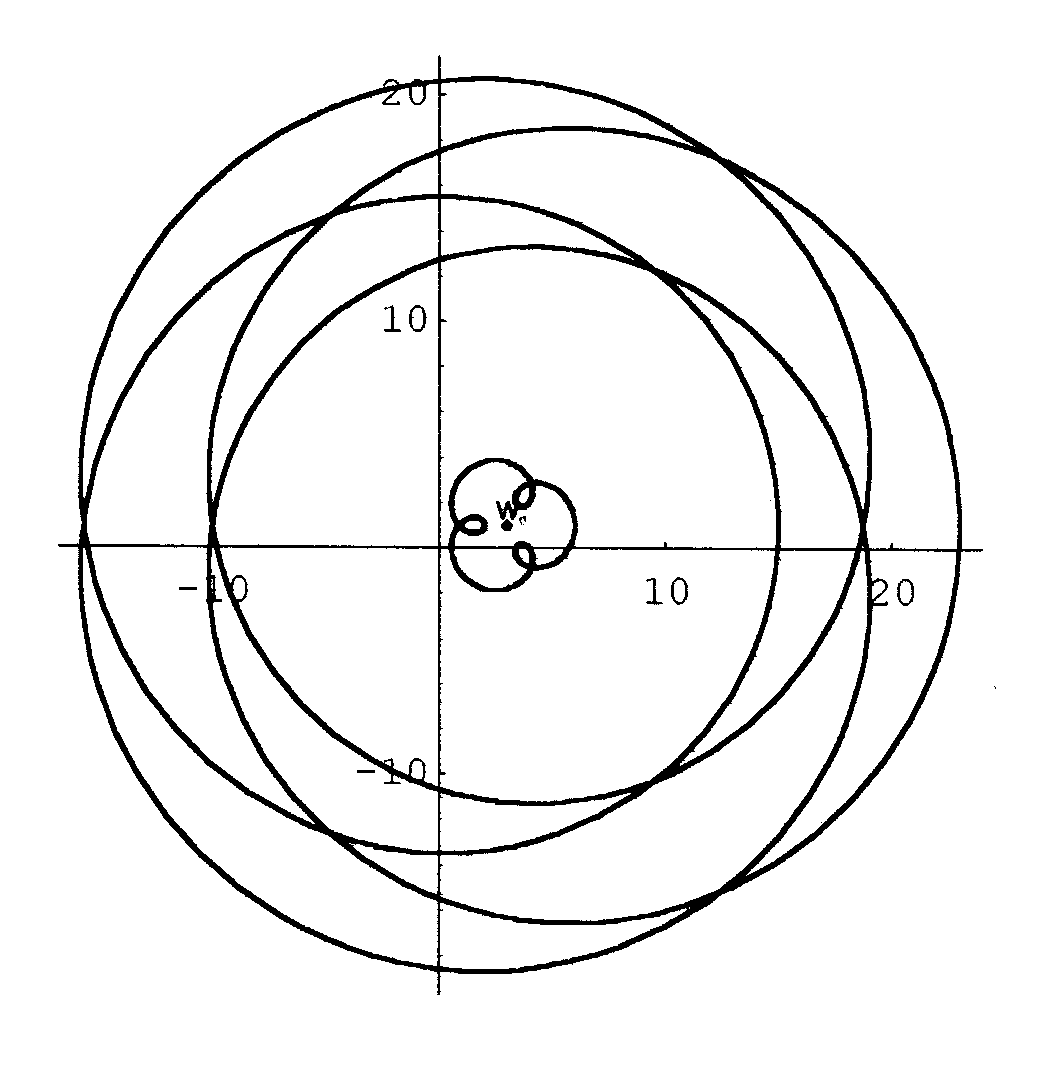
Fig.6 Fig.7

Das Bild besteht aus 4 Umdrehungen. Der Punkt wird einmal, der Ursprung keinmal umschlungen. Nach dem vorangegangenen Beispiel 5 leuchtet ein, dass nicht nur der Punkt 3+i, sondern auch der Ursprung 4-mal umschlungen werden kann, wenn man nur den Radius genügend groß wählt. Für z.B. ergibt sich das Bild in Fig.7. (Zum Vergleich ist wieder das Bild des Einheitskreises eingetragen.)

Unsere anschauliche Vorstellung von Stetigkeit sagt uns nun, dass bei stetiger Veränderung des Radius von r=1.9 zu r=1 sich die Bildkurve stetig verändert von Fig.7 zu Fig.6. Wenn das so ist, muss die Bildkurve (mindestens einmal, höchstens viermal) den Ursprung überstreichen und damit existierte ein (höchstens 4) , für das ist.

Tatsächlich passiert dies das erste Mal für , wie Fig.8 zeigt:

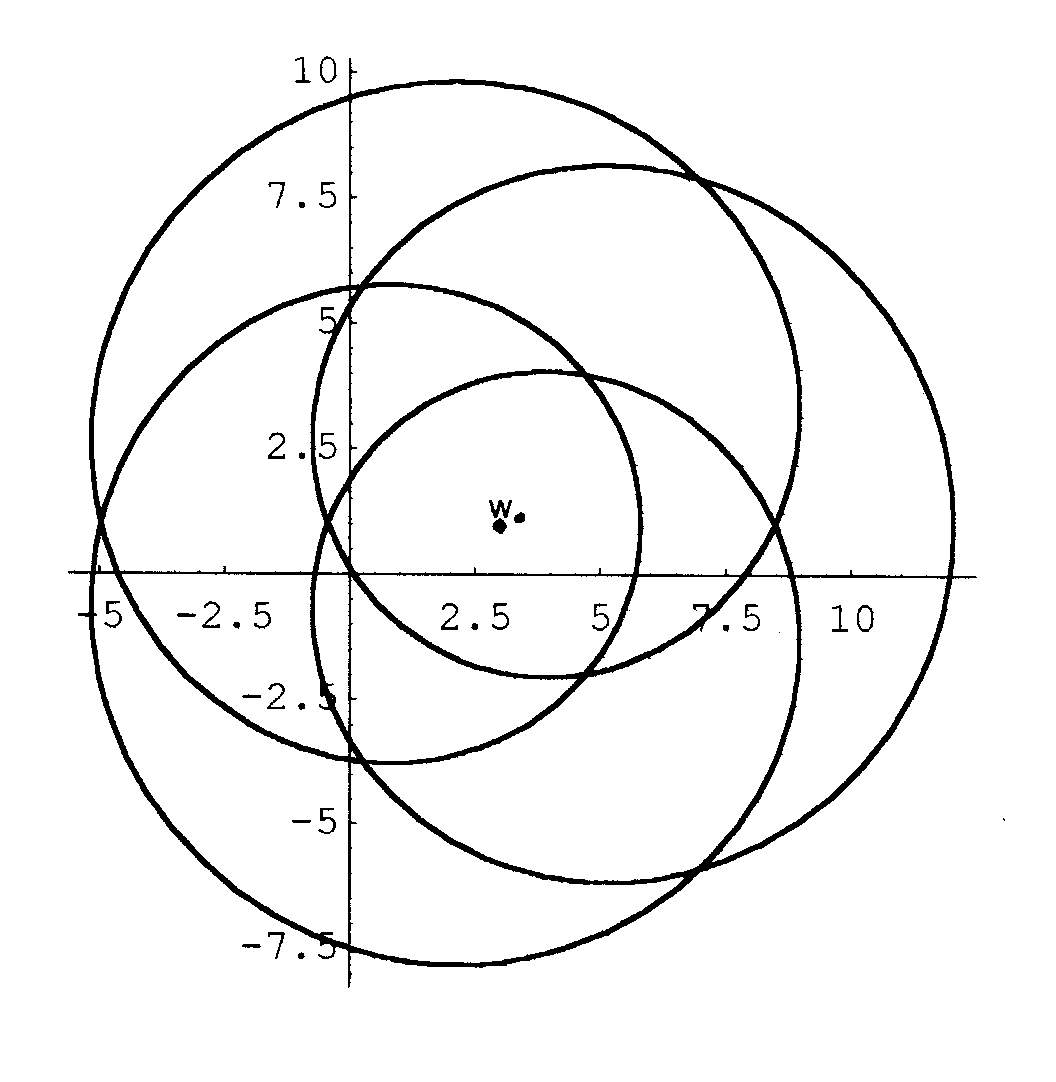
Zurück zur Homepage